Teoria de anillos algebraicos

🧩 1. Definición de anillo

Un anillo (A,+,\cdot) es un conjunto no vacío con dos operaciones binarias:

  • (A,+) es un grupo abeliano (tiene elemento neutro 0, inversos y es conmutativo).
  • (A,\cdot) es un semigrupo (asociativo).

Se cumple la distributividad de la multiplicación respecto a la suma:

a\cdot(b+c)=a\cdot b+a\cdot c \quad \text{y} \quad (a+b)\cdot c=a\cdot c+b\cdot c

👉 Si además existe un elemento 1 tal que 1\cdot a=a\cdot1=a, decimos que tiene unidad.

👉 Si además a\cdot b=b\cdot a para todo a,b, decimos que es conmutativo.

________________________________________________________________________________________________________

🔸 Tipos de anillos

TipoCondición adicional
Anillo con unidadExiste 1\neq 0 tal que 1\cdot a=a\cdot1=a
Anillo conmutativoab=ba para todo a,b
Dominio de integridadConmutativo, con 1\neq 0 y sin divisores de cero
CuerpoTodo elemento no nulo es invertible
Dominio euclídeoDominio de integridad con división con resto

🧠 Resumen visual

  • Todos los cuerpos son dominios de integridad.
  • Todos los dominios de integridad son anillos conmutativos con unidad.
  • No todos los anillos conmutativos son dominios (p. ej. $\mathbb{Z}_6$).
  • No todos los anillos tienen unidad (p. ej. $2\mathbb{Z}$).

🧭 Mapa conceptual: jerarquía de estructuras algebraicas

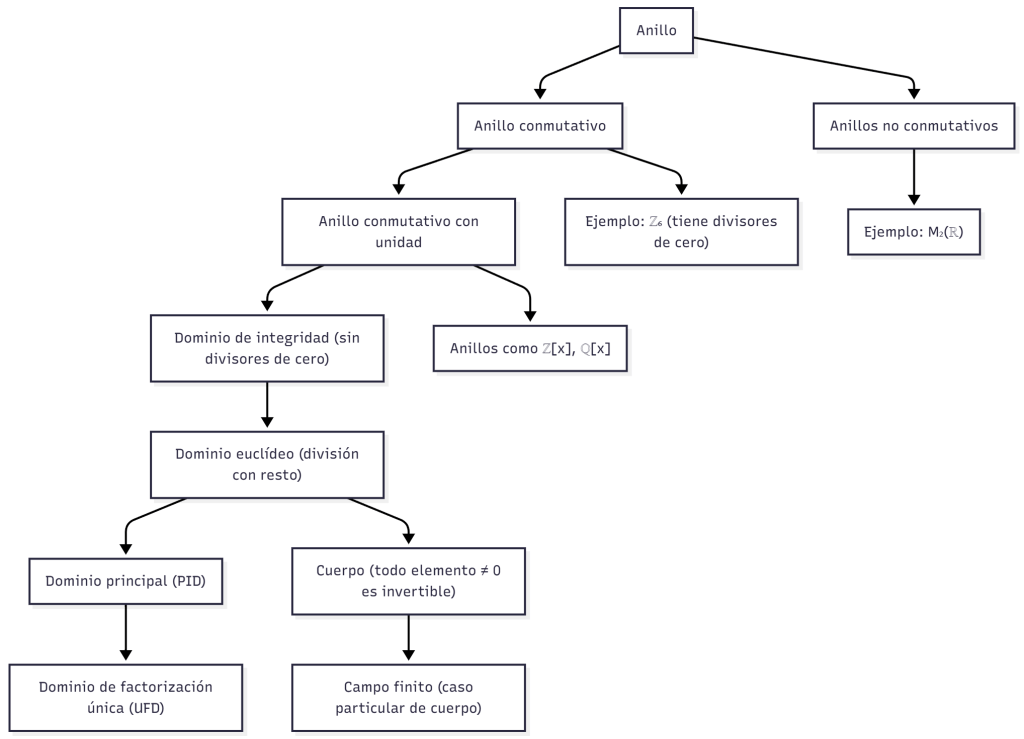
🧱 De los anillos a los cuerpos

Podemos ver las estructuras algebraicas como niveles de organización.
Cada nivel agrega propiedades nuevas a los anteriores:

🧩 Descripción jerárquica

NivelNombrePropiedad claveEjemplo típico
1AnilloSuma y producto distributivos$M_2(\mathbb{R})$
2Anillo conmutativo$ab=ba$$\mathbb{Z}$
3Anillo con unidadExiste $1\neq 0$$\mathbb{Z}, \mathbb{Z}_n$
4Dominio de integridadSin divisores de cero$\mathbb{Z}, \mathbb{Z}[i]$
5Dominio euclídeoDivisión con resto$\mathbb{Z}, \mathbb{Z}[i], F[x]$
6Dominio principal (PID)Todo ideal generado por un solo elemento$\mathbb{Z}, F[x]$
7UFD (factorización única)Factorización única en irreducibles$\mathbb{Z}, F[x]$
8Cuerpo / CampoTodo no nulo es invertible$\mathbb{Q}, \mathbb{R}, \mathbb{Z}_p$

💬 Interpretación intuitiva

  • Cada flecha hacia abajo agrega más “orden” algebraico.
  • Todos los cuerpos son dominios de integridad, pero no al revés.
  • Todo dominio euclídeo es PID, y todo PID es UFD.
  • No todos los dominios de integridad son euclídeos (por ejemplo, $\mathbb{Z}[x]$).

🧠 Resumen rápido

PropiedadSí enNo necesariamente en
Conmutatividad\mathbb{Z}, \mathbb{Z}_nM_2(\mathbb{R})
Unidad\mathbb{Z}, \mathbb{Z}_n2\mathbb{Z}
Sin divisores de cero\mathbb{Z}, \mathbb{Z}_p\mathbb{Z}_6
División con resto\mathbb{Z}, F[x]\mathbb{Z}[x]
Inversos para todos los no nulos\mathbb{Q}, \mathbb{Z}_p\mathbb{Z}

🧠 Conclusión:
Los anillos son la base del edificio.
A medida que agregamos condiciones (unidad, conmutatividad, ausencia de divisores de cero, divisibilidad, etc.),
vamos subiendo hacia estructuras más “perfectas” como los campos y los cuerpos finitos,
donde la aritmética se comporta como los números racionales.

🧮 2. Ejemplos clásicos

AnilloConmutativoTiene unidadObservaciones
\mathbb{Z}✅✅Dominio de integridad
M_n(\mathbb{R})❌✅No conmutativo
\mathbb{Z}_n✅✅Con divisores de cero si $latextlatex n$ no es primo
2\mathbb{Z}✅❌No tiene unidad
{0}✅✅ (por convención)

💣 3. Anillo cero o trivial

El anillo trivial tiene un solo elemento $latext 0$, que cumple:

0+0=0, \quad 0\cdot0=0

Se lo llama también anillo nulo o anillo degenerado.
Matemáticamente simple, emocionalmente vacío 😅.

🔁 4. Anillo de endomorfismos

Sea (G,+) un grupo abeliano.
El conjunto de endomorfismos de G (funciones de G en G que preservan la suma) forma un anillo:

End(G)={f:G\to G \mid f(a+b)=f(a)+f(b)}

con las operaciones:

(f+g)(x)=f(x)+g(x), \quad (f\circ g)(x)=f(g(x))

👉 Este anillo no es conmutativo en general, pero tiene unidad: la identidad id_G.

Ejemplo:
Si G=\mathbb{Z}, entonces todo endomorfismo está dado por f_k(n)=kn, y End(\mathbb{Z})\cong\mathbb{Z}.

⚡ 5. Divisores de cero y dominio de integridad

Un divisor de cero en un anillo A es un elemento a\neq0 tal que existe b\neq0 con:

ab=0

Un dominio de integridad es un anillo conmutativo con unidad sin divisores de cero.

👉 En un dominio de integridad, vale la cancelación:
si ab=ac y a\neq0, entonces b=c.

Ejemplo:

  • $\mathbb{Z}_6$: 2\cdot3=0 \ (\text{mod }6) → no es dominio.
  • $\mathbb{Z}_5$: sin divisores de cero → sí es dominio.

💀 6. Elementos nilpotentes y anillos reducidos

Un elemento a es nilpotente si existe n>0 tal que a^n=0.

El conjunto de todos los nilpotentes de un anillo A forma el radical nil.

Un anillo se llama reducido si no tiene elementos nilpotentes distintos de 0.

Ejemplo:

  • En $\mathbb{Z}_4$, 2^2=0 → no es reducido.
  • En $\mathbb{Z}_6$, ningún a\neq0 tiene a^n=0 → reducido.

🧠 Ejercicios para hacer a mano

Determinar si los siguientes conjuntos con las operaciones usuales son anillos:

a) 2\mathbb{Z}
b) \mathbb{Z}_6
c) M_2(\mathbb{R})
d) \mathbb{Z}[x]

Identificar los divisores de cero en \mathbb{Z}_{12}.

Decidir cuáles son dominios de integridad:

a) \mathbb{Z}_7
b) \mathbb{Z}_8
c) \mathbb{Z}[x]

Probar que en un dominio de integridad vale la ley de cancelación.

En \mathbb{Z}_9, encontrar todos los nilpotentes.

📜 Nota histórica

Los anillos nacen a fines del siglo XIX como una abstracción de la aritmética de enteros y polinomios, pero el término Ring fue introducido por Emmy Noether en 1921 💪.
Antes se hablaba de “cuerpos de integridad” o “dominios numéricos”.

Noether fue quien le dio la forma axiomática moderna al concepto,
y además revolucionó el álgebra conmutativa y la topología algebraica.
O sea: fue la Gauss de la era moderna.

Deje un comentario

Blog de WordPress.com.

Subir ↑